こんにちは。
ちょっと前にAOJの問題を解いて動的計画法を学びましたが↑、グラフも勉強しようかなって思ってグラフのページを開きました。1番最初にあったのが
です。何も知らない僕は最初幅優先探索でやりましたがWAになるのでwikipediaを調べたところ
単一始点最短経路問題 (SSSP:Single Source Shortest Path)
特定の1つのノードから他の全ノードとの間の最短経路問題。この問題を解くアルゴリズムとしては、ダイクストラ法やベルマン-フォード法がよく知られている。
最短経路問題 - Wikipedia
とのことだったので、前から噂には聞いていたけどやったことのないダイクストラ法に挑戦することにしました 。
- 挑戦前のレベル
DFSやBFSが一応はわかるくらいにグラフを扱ったことがある
今回主に参考にしたのは ダイクストラ法が分からなかった君のために - kuuso1のブログ です。
問題
(単一始点最短経路から一部改変)
与えられたグラフと始点 $r$ について、単一始点最短経路の重みを求めるプログラムを作成してください。ノード $r$ を始点とし、$r$ から各ノードについて、最短経路上の辺の重みの総和を出力してください。
入出力
- 入力
\begin{align} &V \quad E \quad r\cr &s_0 \quad t_0 \quad d_0\cr &s_1 \quad t_1 \quad d_1\cr &:\cr &s_{E-1} \quad t_{E-1} \quad d_{E-1} \end{align}
ここで $V,E$ はグラフの頂点と辺の数。 グラフの頂点にはそれぞれ $0,1,...,V−1$ の番号が付けられている。$r$は始点の番号である。$s_i, t_i$ はグラフの $i$ 番目の辺が結ぶ2つの頂点を表す(有向)。$d_i$ は $i$ 番目の辺の重みである。
- 出力
$i$ 行目に $r→i$ の最短経路長を出力する
制約
- $1 \le V \le 100000$
- $0 \le d_i \le 10000$
- $0 \le E \le 500000$
- グラフに平行辺はない
- グラフに自己ループはない
ダイクストラ法の実践
悩んだが説明できる気がしないので、「何をしたいか」をグラフを使って見せていきます。使うグラフはダイクストラ法が分からなかった君のために - kuuso1のブログで使われているグラフです。

四角に入っているのが始点(頂点0)からの距離(の初期値)です。(以下、「距離」と言ったら「始点からの距離」です)
その2の方法の良く知られた高速化として、最小コストが更新される可能性のある場合だけキューに追加するというものがあります。これはキューにたまるゴミが減ることがもたらす効果になります。
ダイクストラ法が分からなかった君のために - kuuso1のブログ
の次に載っているgifの操作をグラフ上に示したのが以下のgifです。
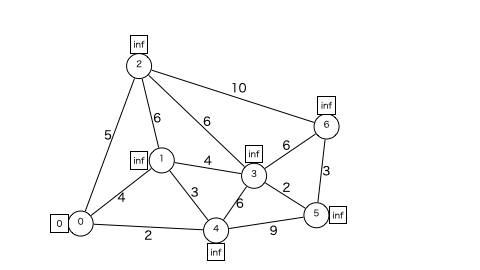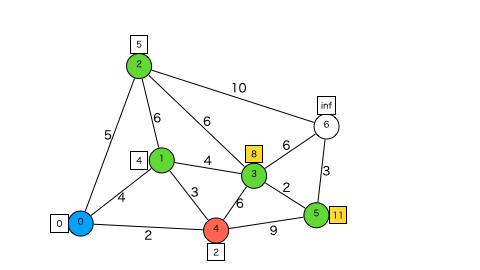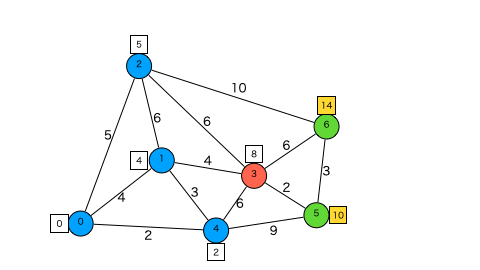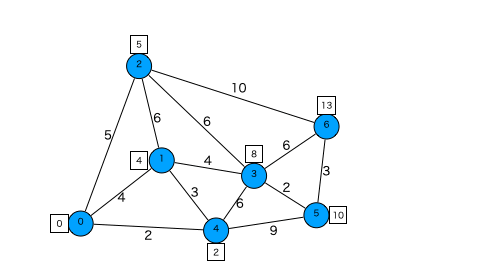
赤い頂点は今注目している頂点で、緑の頂点が探索キューに入っている頂点です。距離の四角が黄色くなったとき頂点の最短距離(暫定値)が更新され、頂点が青くなったら距離確定です。
やっていることは
- 探索キューに入っている(緑色の)頂点の中から距離が最短のものを選ぶ
- 選んだ頂点から行ける頂点について、最短距離が更新できるなら更新し、その頂点を探索キューに入れる
- 選んでいた頂点を距離確定にする(確定したことを明示する必要は実はないけど*1)
の繰り返しです。細かいところも含めて1ステップずつみていきます。
探索キューは、{頂点の番号と距離}のペアを入れた優先度付きキューで、頂点の距離が小さいものから取り出すようにしています。
- ステップ1

頂点0をキューに入れます
| Node | 0 |
|---|---|
| dist | 0 |
- ステップ2

頂点0を取り出し、行ける頂点{1,2,4}の距離を更新してキューに入れます
| Node | 4 | 1 | 2 |
|---|---|---|---|
| dist | 2 | 4 | 5 |
- ステップ3

頂点0は前のステップで処理が終わったので確定です(以下同様)
頂点4を取り出し、行ける頂点{0,1,3,5}をチェックしますが、頂点{0,1}は頂点4を経由すると距離が伸びてしまうので無視します。よって頂点{3,5}の距離を更新してキューに入れます
| Node | 1 | 2 | 3 | 5 |
|---|---|---|---|---|
| dist | 4 | 5 | 8 | 11 |
- ステップ4
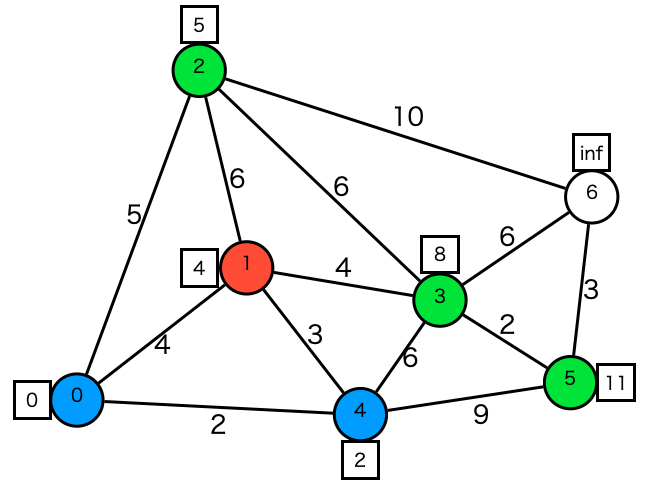
頂点1を取り出し、行ける頂点{0,2,3,4}をチェックしますが、更新できる頂点がないのでキューへの追加はなしです
| Node | 2 | 3 | 5 |
|---|---|---|---|
| dist | 5 | 8 | 11 |
- ステップ5

頂点2を取り出し、行ける頂点{0,1,3,6}をチェックします。更新できるのは頂点6のみです。
| Node | 3 | 5 | 6 |
|---|---|---|---|
| dist | 8 | 11 | 15 |
- ステップ6
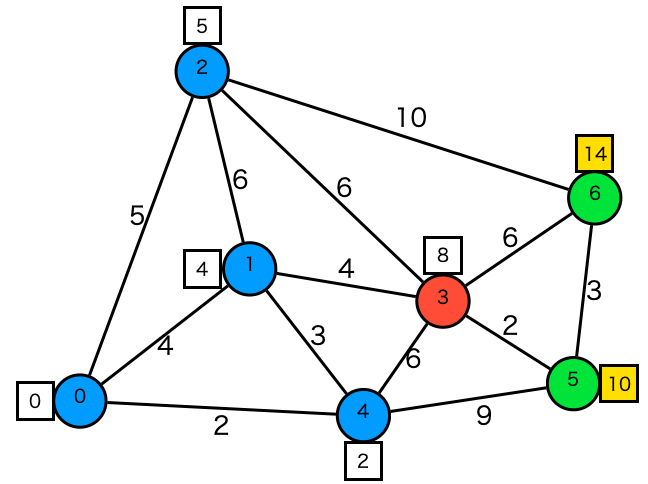
頂点3を取り出し、行ける頂点{1,2,4,5,6}をチェックします。更新対象は頂点{5,6}です。
| Node | 5 | 5 | 6 | 6 |
|---|---|---|---|---|
| dist | 10 | 11 | 14 | 15 |
キューの中身を((5,11)→(5,10)のように)直接書き換えられれば良いのですが難しいのでとりあえず新しい(頂点,距離)のペアを投入します。
- ステップ7
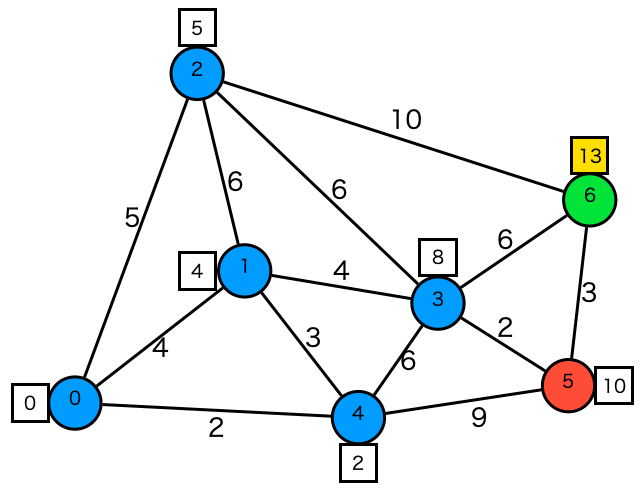
頂点5を取り出し、行ける頂点{3,4,6}をチェックします。頂点6の距離を更新します。
| Node | 5 | 6 | 6 | 6 |
|---|---|---|---|---|
| dist | 11 | 13 | 14 | 15 |
- ステップ7.5
グラフ上には現れていませんがここでキューから「暫定距離11の頂点5」を取り出しています。ただ、すでに頂点5の距離は長くても10とわかっているので無視します(頂点5の距離が11だと仮定して計算しても何も得しない)。
| Node | 6 | 6 | 6 |
|---|---|---|---|
| dist | 13 | 14 | 15 |
- ステップ8
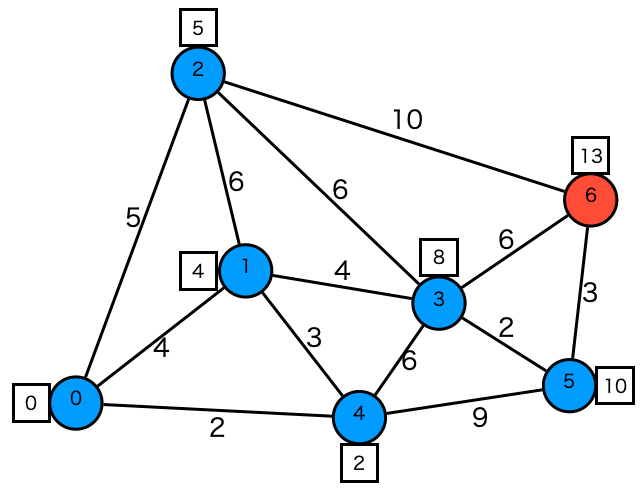
頂点6を取り出し、行ける頂点{2,3,5}をチェックしますが更新できるところはないです。
| Node | 6 | 6 |
|---|---|---|
| dist | 14 | 15 |
- ステップ9
グラフには現れていませんがキューに残った「暫定距離14の頂点6」と「暫定距離15の頂点6」を取り出し(て無視し)たら、キューが空になるので終了です。

実装
先ほどのグラフに必要なエッセンスは入っているので実装していきます。
- 下準備
グラフの辺は、行き先と重みのpairとし、グラフは、各頂点ごとに出てる辺を格納する隣接リストで表現します。各頂点の距離を入れるvector<ll> distも用意します。
#include <bits/stdc++.h> using namespace std; using ll = long long; #define INF 1LL<<60 using Edge = pair<ll, ll>; //辺 using Graph = vector<vector<Edge>>; //隣接リスト ll V,E,r; Graph G; vector<ll> dist;
- ダイクストラ法本体の実装
入力のことは後で考えるとして本体を書いていきます。
void dijkstra(){ priority_queue< pair<ll, ll>, vector<pair<ll, ll>>, greater<pair<ll, ll>> //{距離, 頂点}のpairで格納 //距離の小さいものから取り出す >que; que.push({0, r}); //距離0の頂点rを入れる while(!que.empty()){//キューが空になるまで auto now = que.top(); que.pop(); //キューの先頭を取り出す ll nowDist = now.first; //取り出した距離 ll nowNode = now.second; //取り出した頂点 for(Edge next: G[nowNode]){ //行ける頂点について ll nextDir = next.first; //辺の行き先 ll nextWeight = next.second; //辺の重み dist[nextDir] = min(dist[nextDir], dist[nowNode] + nextWeight); //更新する que.push({dist[nextDir], nextDir}); //キューに追加 } } }
まず、ステップ1, 2の処理ができるようになりました。
優先度付きキューについて、priority_queue - cpprefjp C++日本語リファレンスに書いてある通りに処理順のカスタマイズをしました。priority_queueは末尾から順番に取り出すので、比較関数の使い方に注意が必要です。
次に、ステップ3でやっている、キューへの追加をスルーする処理をつけます。
void dijkstra(){ priority_queue< pair<ll, ll>, vector<pair<ll, ll>>, greater<pair<ll, ll>> >que; que.push({0, r}); while(!que.empty()){ auto now = que.top(); que.pop(); ll nowDist = now.first; ll nowNode = now.second; for(Edge next: G[nowNode]){ ll nextDir = next.first; ll nextWeight = next.second; if(dist[nextDir] <= dist[nowNode]+nextWeight)continue; //更新しても距離を小さくできないときスルーする dist[nextDir] = dist[nowNode] + nextWeight; que.push({dist[nextDir], nextDir}); } } }
次に、ステップ7.5で行った、「キューから取り出した情報を無視する場合」の処理を加えます
void dijkstra(){ priority_queue< pair<ll, ll>, vector<pair<ll, ll>>, greater<pair<ll, ll>> >que; que.push({0, r}); while(!que.empty()){ auto now = que.top(); que.pop(); ll nowDist = now.first; ll nowNode = now.second; if(nowDist > dist[nowNode])continue; //取り出した距離が、今現在わかっている頂点の距離より長い時スルーする for(Edge next: G[nowNode]){ ll nextDir = next.first; ll nextWeight = next.second; if(dist[nextDir] <= dist[nowNode]+nextWeight)continue; dist[nextDir] = dist[nowNode] + nextWeight; que.push({dist[nextDir], nextDir}); } } }
これでダイクストラ法の本体は完成です。あとは入出力をするメイン関数を書きます。これは特にコメントは無いですね
int main(){ cin>>V>>E>>r; G.resize(V); for(int i=0; i<E; i++){ int s,t,d; cin>>s>>t>>d; G[s].push_back({t, d}); } dist.resize(V, INF); dist[r] = 0; dijkstra(); for(ll x: dist){ if(x==INF){ cout<<"INF"<<endl; }else{ cout<<x<<endl; } } }
完成
以上をつなぎ合わせて完成です
https://o-treetree.hatenablog.com/entry/GRL1A
AC確認済み→https://onlinejudge.u-aizu.ac.jp/status/users/ohys/submissions/1/GRL_1_A/judge/4549329/C++14
ちなみに、今回使ったグラフは次の入力で試すことができます
(AOJの入力が有向グラフ仮定なので、例の無向グラフを表現するためにそれぞれの辺を向きを変えて2回入力します)
参考
- ダイクストラ法が分からなかった君のために - kuuso1のブログ
- priority_queue - cpprefjp C++日本語リファレンス
- https://qiita.com/y_shindoh/items/17d9fa334a2cb8e74bfa
*1:確定したとき、その頂点までの最短経路にある頂点も全て確定しているので、他のところから迂回してくる経路では最短を更新できない